Eight scientists analyzed the article and estimated its overall scientific credibility to be ‘very low’. more about the credibility rating
A majority of reviewers tagged the article as: Biased, Cherry-picking, Flawed reasoning, Misleading.
SCIENTISTS’ FEEDBACK
SUMMARY
This article at Breitbart argues that World Health Organization rankings of particulate matter air quality show that the United States is not one of the biggest polluters in the context of the Paris Agreement. Scientists who reviewed the article explain that this is misleading. Air quality is not an indication of national greenhouse gas emissions—and the United States is currently the second-largest emitter of carbon dioxide. This is true regardless of whether one uses the term “pollution” to describe carbon dioxide emissions.
See all the scientists’ annotations in context
REVIEWERS’ OVERALL FEEDBACK
These comments are the overall opinion of scientists on the article, they are substantiated by their knowledge in the field and by the content of the analysis in the annotations on the article.
Michael Brauer, Professor, The University of British Columbia:
The facts in the article are correct but the entire premise is deliberately misleading—it is correct that with respect to CONCENTRATIONS (i.e. the level is in the air) of one type of health-damaging air pollutant, the US is one of the countries with the lowest concentrations in the world. However, the Paris Accord is related to EMISSIONS (how much is released into the air) of climate-forcing pollutants and in that context the U.S. is among the countries in the world with both the highest overall emissions and the highest emissions per capita (higher than all other OECD countries). For climate change, EMISSIONS are what matters.
Aimée Slangen, Researcher, Royal Netherlands Institute for Sea Research (NIOZ):
This whole post is based on semantics and basically one big strawman fallacy. The author is deliberately confusing air pollution from suspended particulate matter (as discussed in the WHO report) with pollution from carbon dioxide emissions (as discussed in the Reuters link and the Paris Agreement). Even though CO2 does not impact our health through “disease-causing pollutants that get into people’s lungs”, it does change our environment and the Earth’s climate, and in that sense does classify as a pollutant.
Pierre Friedlingstein, Professor, University of Exeter:
Deliberately misleading about the role of CO2 and whether it is a pollutant or not, minimizing the role of CO2 as a greenhouse gas agent leading to climate change.
Dan Jones, Physical Oceanographer, British Antarctic Survey:
Should we call carbon dioxide a “pollutant”? That question is relevant for policy, but either way, our choice of language does not change how physics behaves. When you add more carbon dioxide to Earth’s lower atmosphere, you get more energy at Earth’s surface. The extra energy added by human emissions of CO2 has to go somewhere; it isn’t going to just disappear. It ends up in the ocean, atmosphere, and cryosphere, affecting Earth’s climate system and putting us at risk for negative climate impacts (e.g. sea level rise, heat waves of increasing frequency and intensity, shifts in precipitation patterns). The author claims that this additional warming might actually be beneficial overall, which is inconsistent with the body of scientific literature on the topic (as always, see IPCC for summary).
In short, this article makes a number of misleading statements and casually dismisses volumes of scientific evidence.
Alexis Berg, Research Associate, Harvard University:
This article willingly confuses air pollution by particulate matter and greenhouse gas emissions. The article cherry-picks skeptic claims and out-of-context scientific evidence like deep-past CO2 atmospheric levels to try to make the case that CO2 emissions and climate change are not an issue. It tries to deny the fact that the US is a large climate change “polluter”, in the sense that it emits a lot of greenhouse gas per capita, by using the old, tired talking point that CO2 is not a pollutant, and that otherwise US air pollution is pretty low. Irrelevant and misleading.
Notes:
[1] See the rating guidelines used for article evaluations.
[2] Each evaluation is independent. Scientists’ comments are all published at the same time.
KEY TAKE-AWAYS
The statements quoted below are from the article; comments and replies are from the reviewers.
“Despite recent attempts to paint the United States as a major global polluter, according to the World Health Organization (WHO), the U.S. is among the cleanest nations on the planet.”
Pierre Friedlingstein, Professor, University of Exeter:
This Breitbart article is playing with words, arguing that CO2 is not a “pollutant”. When it comes to CO2, the US is the second largest emitter after China. CO2 is a greenhouse gas, primarily responsible for climate change, inducing negative impacts on human and ecosystems. Replace the word “polluter” with “emitter” and the whole article falls apart—there is no story here.
Chris Brierley, Senior Lecturer, University College London:
This presumes a strong link between the cleanliness of a country’s air and its own emissions. This does not necessarily hold. For example, the tiny papal state of the Vatican City is probably rather polluted (as it’s contained solely within the city of Rome). However, the vast majority of that pollution will have been emitted in Italy.
“While France and other G7 countries lamented the U.S. exit from the Paris climate accord, America’s air is already cleaner than that of any other country in the G7, except Canada with its scant population.”
Pierre Friedlingstein, Professor, University of Exeter:
The Breitbart author must know that the Paris Agreement is about climate change, not about air quality.
“the WHO measures air pollution by the mean annual concentration of fine suspended particles of less than 2.5 microns in diameter. These are the particles that cause diseases of all sorts and are responsible for most deaths by air pollution.
According to the WHO, exposure to particulate matter increases the risk of acute lower respiratory infection, chronic obstructive pulmonary disease, heart disease, stroke and lung cancer.
The report […] found that the United States was one of the most pollution-free nations in the world.”
Daniel Cohan, Associate Professor, Rice University:
The particulate matter (PM) discussion is essentially correct. PM is indeed thought to cause far more deaths than any other air pollutant. The United States indeed has lower PM2.5 levels than most other countries, especially when comparing cities. Most of the country outside California attains EPA’s 12 ug/m3 PM2.5 standard.
“Most pollution-free” is poorly worded, since of course no populated area is ‘pollution-free’. But yes, PM2.5 levels in urban and rural areas of the United States are lower than those in corresponding areas of many other countries.
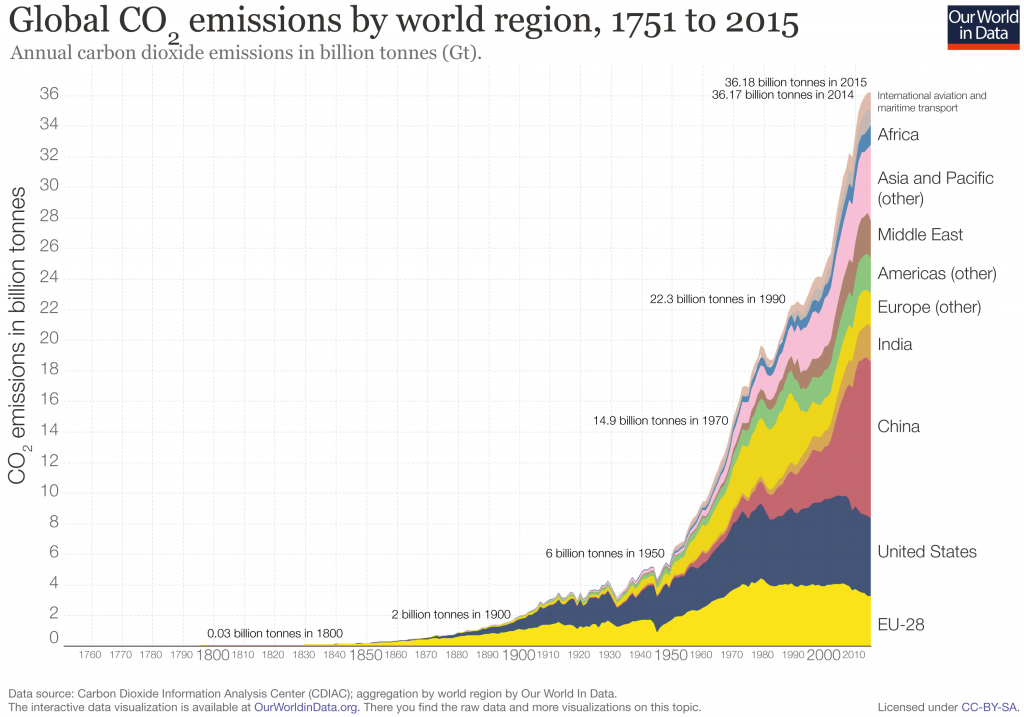
The article misleads by conflating levels of air pollution with terminology like “most polluting” or “biggest polluters”. Relatively clean air quality in the United States does not negate the fact that we are the world’s second largest emitter of CO2.
“With such relatively clean air throughout America, how can even reputable news agencies like Reuters continue spreading the well-worn lie that the United States is one of the ‘biggest polluters’ in the world?”
Pierre Friedlingstein, Professor, University of Exeter:
Reuters is simply saying that in terms of CO2 emissions, China is the top emitter and the USA is second. There is no point denying this. It’s a fact, based on national fossil fuel production and consumption inventories. Whether you call CO2 “pollutant” or not is irrelevant. It is the main driver of climate change.
Chris Brierley, Senior Lecturer, University College London:
America has the largest economy and the 3rd largest population on Earth. Even if each of its factories and people themselves emitted less than in most other countries, it would still add up to being one of the biggest polluters.
Alexis Berg, Research Associate, Harvard University:
As the author pretends not to understand, this is the case if one considers greenhouse gas emissions as part of pollution. While China’s emissions grew tremendously over the last couple decades and it overtook the US as the largest total emitter a few years ago, the US is still one of the largest emitters per capita.

In addition, historically, the US (and the EU) still own the largest share of cumulative emissions since the preindustrial era when emissions began.
“While the United States must remain vigilant to keep the level of real, dangerous pollutants to a minimum, it may take some consolation in the fact that among G7 nations, it has the cleanest air of all.”
Chris Brierley, Senior Lecturer, University College London:
Carbon dioxide is a well-mixed greenhouse gas—its concentrations are roughly 407 ppm everywhere across the globe. The national concentration bears absolutely no relevance to the country’s emissions.
“The problem with this ploy is that carbon dioxide is not a pollutant and it is dishonest to say it is. CO2 is colorless, odorless and completely non-toxic. Plants depend on it to live and grow, and human beings draw some into their lungs with every breath they take to no ill effect whatsoever.
Growers regularly pump CO2 into greenhouses, raising levels to three times that of the natural environment, to produce stronger, greener, healthier plants.”
Pierre Friedlingstein, Professor, University of Exeter:
Again, the point is not “is CO2 a pollutant or not”. (I believe the Supreme Court said it is.) The point is: CO2 emissions in the atmosphere lead to climate change as CO2 is a greenhouse gas. Climate change has and will have negative impact on ecosystems (land and ocean). The author deliberately ignores this.
Aimée Slangen, Researcher, Royal Netherlands Institute for Sea Research (NIOZ):
While the CO2 does not impact our health through “disease-causing pollutants that get into people’s lungs”, it does change our environment and the Earth’s climate, and in that sense it does classify as a pollutant.
Richard Lindroth, Vilas Distinguished Achievement Professor, University of Wisconsin-Madison:
This statement is absolutely ridiculous. It violates the most basic, fundamental maxim of toxicology, first articulated by the Renaissance physician Paracelsus:
“The dose makes the poison.” Or, “All things are poison and nothing is without poison; only the dose makes a thing not a poison.”
In other words, just because a substance at one concentration is harmless does not mean it is harmless at another concentration. We don’t normally think of consumption of water as harmful to humans, but at high enough doses it will kill—and has done so.
A pollutant is generally defined as a substance—artificial (synthetic) or natural—that occurs in the environment at least in part because of human activity, and that has a deleterious impact on living systems.
Given that basic definition, there is no way that CO2 can not be a pollutant. It is produced by a variety of human activities, but principally burning of fossil fuels. Increases in its concentration are clearly linked to global warming, which has already, and increasingly will, negatively affect living systems, including humans. The only exit from this logic is to deny that CO2 leads to warming (in contradiction to massive scientific evidence) or to deny that warming negatively impacts living systems (again in contradiction to massive evidence).
The authors use a classic rhetorical ploy to confound bits of information and draw erroneous conclusions. Yes, at low concentrations CO2 is not directly harmful to humans, and in fact is required by plants. And yes, small increases in CO2 have been shown to increase plant growth. (Some of my own work has shown such; such increases also shift the chemical composition of plant tissues, and not always for the better!). Plants grown under elevated CO2 do grow faster. To my knowledge, there is no evidence that they are “stronger” (whatever that means), and if anything, they are less green. Nor is there convincing evidence they are healthier. If anything, insects consume them more than ambient-CO2 plants.
Alexis Berg, Research Associate, Harvard University:
This depends on the definition of “pollutant”. To the extent that CO2-induced global warming endangers human welfare and health, CO2 fits the Clean Air Act’s broad definition of “air pollutants”—that’s the reasoning behind the Supreme Court’s decision to let the EPA regulate CO2 emissions.
Not that this is relevant to the definition of CO2 as a pollutant (which relies on it causing climate change), but the alleged total non-toxicity is not entirely true: there is some research* showing impairments in cognitive function test scores in people exposed to CO2 concentrations in the 950-1,000 ppm range, and even significantly worse performance when CO2 rose to 1500 and 2,500 ppm. Current atmospheric CO2 is around 400 ppm—possibly going up at least a few more hundred ppm this century without emission cuts—but concentrations greater than ~1000 ppm are often found in poorly ventilated rooms and buildings.
- Allen et al (2016) Associations of cognitive function scores with carbon dioxide, ventilation, and volatile organic compound exposures in office workers: a controlled exposure study of green and conventional office environments, Environmental Health Perspectives
“Without human intervention, the concentration of CO2 has climbed as high as 7,000 parts per million (ppm) in prior eras, whereas at present the concentration is just over 400 ppm.”
Pierre Friedlingstein, Professor, University of Exeter:
A CO2 concentration of 7000 ppm is a model estimate (not observations) for the Cambrian, about 500 million years ago. There are obviously no measures of temperature for that time, but estimates from models are about 10°C (18°F) warmer than present day! Not exactly reassuring news…
Chris Brierley, Senior Lecturer, University College London:
But those worlds were rather different to those that humans inhabit. They had things like palm trees and crocodiles in the Arctic, and arguably land in the Tropics was completely sterile because of the heat.
“Some experts, such as UN climate scientist Dr. Indur Goklany, have defended rising CO2 levels as a good thing for humanity. Goklany has argued that the rising level of carbon dioxide in the earth’s atmosphere ‘is currently net beneficial for both humanity and the biosphere generally.”
Chris Brierley, Senior Lecturer, University College London:
I don’t believe that Dr. Goklany was ever employed or seconded to the UN. In fact, he would appear to be working for the climate-dismissing think tank, the Heartland Institute.
Alexis Berg, Research Associate, Harvard University:
Technically, there is no such thing, really, as a UN climate scientist. There are climate scientists, worldwide, working for universities or national research organizations, and who contribute to the UN’s IPCC review process when it produces its report, every 7 years or so. Dr. Goklany is listed (Wikipedia) as working for the US Department of Interior as a science and technology policy analyst. His PhD is in electrical engineering, and beyond opinion pieces, he doesn’t seem to have published in the field of climate sciences.
So I am not sure why his opinion is relevant at all—it goes without saying that it goes against the assessment of most of the scientific community working on climate change issues.
Pierre Friedlingstein, Professor, University of Exeter:
Dr. Goklany is one of the very few defending that view. IPCC AR5* is very clear: “Continued emission of greenhouse gases will cause further warming and long-lasting changes in all components of the climate system, increasing the likelihood of severe, pervasive and irreversible impacts for people and ecosystems.”

